Home
The Real Kato
Facebook
Frozen Lunches
Links
Kottke
Daring Fireball
Amalah
Secret Agent Josephine
Dooce
Contact
Archives
Most Recent
2026 January
2009 September
2009 August
2009 July
2009 June
2009 May
2009 April
2009 March
2009 February
2009 January
2008 December
2008 November
2008 October
Categories
All Categories
bloggers
books
commentary
dating
food
funnyhaha
interesting
life
movies
music
politics
reviews
science
site-business
sports
style
techwatch
television
theater
travel
Recent Comments
The Real Kato
Frozen Lunches
Links
Kottke
Daring Fireball
Amalah
Secret Agent Josephine
Dooce
Contact
Archives
Most Recent
2026 January
2009 September
2009 August
2009 July
2009 June
2009 May
2009 April
2009 March
2009 February
2009 January
2008 December
2008 November
2008 October
Categories
All Categories

bloggers

books

commentary

dating

food

funnyhaha

interesting

life

movies

music

politics

reviews

science

site-business

sports

style

techwatch

television

theater

travel

Recent Comments
| On College Football 2022: Week 6 Recap and Week 7 Pre... Ken said: |
| Yeah, we've both had our share of hope and disappointment in this game. Let's just hope for a good b... |
| On College Football 2022: Week 6 Recap and Week 7 Pre... Dan* said: |
| I'm not sure how I feel about this game. On one hand, I feel pretty optimistic that we have the tale... |
| On College Football 2022: Week 1 Preview Dan* said: |
| Glad to see you'll be back writing football again, Ken! Congrats on the easy win today. You didn't ... |
| On College Football 2021: Week 10 Recap and Week 11 P... Ken said: |
| Yeah, sorry one of our teams had to lose. I've come to appreciate Penn State as a classy and sympath... |
| On College Football 2021: Week 10 Recap and Week 11 P... Dan* said: |
| Hey Ken, congratulations on the win yesterday! Some really odd choices by our coaching staff in that... |
<< Previous: College Football Rec... | Next: College Football Rec... >>
| The Great Escalator Versus Stairs Debate | Sunday, 2009 September 27 - 3:17 pm |
| I had an interesting discussion with some co-workers a while back. The question posed was: if you walk up an escalator that's going down (i.e., you go the wrong way on a down escalator, at an upward speed exactly opposite the downward speed of the escalator), would that give you the same amount of exercise as if you walked the equivalent number of stationary stairs? The immediate intuitive answer among most of us (an educated group of engineers) was "no", for two reasons: first, on an escalator, the bulk of your body mass is not moving relative to the earth and relative to gravity; second, if you actually ascend stairs, you must be expending energy in return for the potential energy that you gain. (If you don't remember your high school physics: something that sits at the top of a hill has potential energy, equivalent to the kinetic energy it would have if it rolled to the bottom of the hill.) 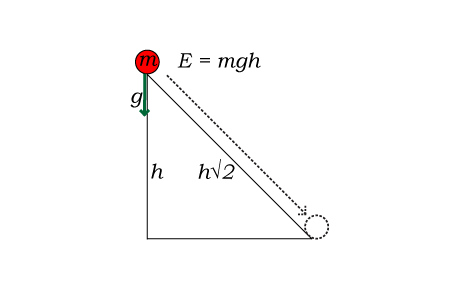 But one guy, Tim Ross, took the opposite stand, arguing that it must be equivalent, and I give him credit for sticking to that despite other people's arguments to the contrary. His primary argument was this: if you were in a large room with a staircase, and the entire room was moving at a constant speed in a diagonally downward direction, you'd feel exactly like you were climbing a stationary set of stairs. Think of being in an elevator in a tall building: you only sense when the elevator starts or stops; while it's traveling at a constant speed between floors, it feels like you're standing still.  So how to reconcile this paradox? Let's consider the original reasons we said "no, it's not the equivalent amount of exercise". The first was that on an escalator, you're not moving your body mass against gravity. While this is true, the problem with this argument is that it doesn't take energy to move mass, it takes energy to accelerate it. When you (a body with mass m) take an initial step upward on a stationary stair, you create an upward acceleration of slightly higher than the acceleration of gravity (call it a, where a is greater than g, and g is the acceleration of gravity on earth, 9.8 m/s^2) so that your vertical velocity goes from zero to (a – g)t over a period of time t. Call this velocity v. (We'll only consider the vertical, y-axis, component of motion and acceleration in these equations.) During this time, you've applied a force equal to ma. To continue moving upward in a smooth motion, you have to continuously provide an upward force equal to mg; any less, and gravity would slow your upward motion back to a halt. 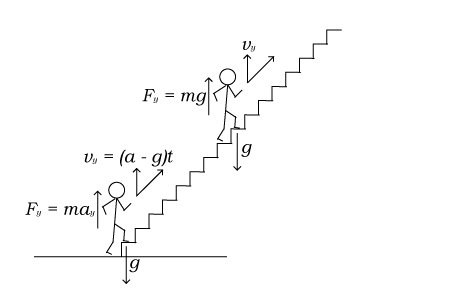 If you're on an escalator that's moving at a downward velocity equal to –v, and you apply the same force ma for the same period of time t, your vertical velocity would go from –v to 0. If you then continue to apply upward force of mg, your vertical velocity remains zero. What's important to note is that you've applied the same force for the same amount of time, using the same muscle motions; so as far as your body knows, you've done the exact same amount of work on the escalator as you have on the stairs. It's noteworthy, though, that this argument doesn't hold if you're allowed to hang on to stationary handrails while walking on the escalator. If so, then your arms are providing a portion of the force (mg) necessary to keep your body at rest, and since there's no muscle motion involved in that, you're expending less effort. On a stationary staircase, the equivalent would be if there were motorized handrails moving up that you could essentially ride upwards. So what about the second argument, regarding the potential energy? Where did that energy go? The short answer is than when you take a step up on the escalator, or just stand still on an escalator step, the force of gravity and the force that you apply to the step are pushing the escalator step downward. The work that your body does on the escalator over a period of time happens to match the work that you'd do climbing the stairs: mgh. The math is a bit complicated here because you have to consider that escalators have motors that are designed to keep the escalator moving at a constant speed, so the forces applied to it don't actually accelerate it but merely change the electrical load on its motors. It may help to think of a person walking on a horizontal conveyor belt instead of an escalator. The really surprising thing about all this is that there doesn't seem to be much analysis of this on the Internet. I have to imagine that it's just because there's not much interest in the subject... but hey, maybe I'll become the definitive Internet reference on this topic for the handful of folks who might be curious about it. |
| Permalink 17 Comment
Posted by Ken in: interesting |
Comments
| Comment #1 from Phil (marsosudiro) 2009 Sep 27 - 11:06 pm : # |
| Okeydokey -- it's late and I'm not 100%, but here's a sketch of my counterargument. You wrote: "The short answer is than when you take a step up on the escalator," and I'm not sure that's actually "happening" when you use the escalator like a treadmill. The short answer from me is that when you do the escalator thing, your center of mass doesn't move (relative to surface your feet are on) in the same way as when you go up a set of stairs. I've done the escalator thing you describe (more than once, for reasons I'm not sure), and what I think happens is that my weight is almost constantly borne by whichever foot is on the upper step, and my center of mass stays fairly close to ~ four feet above the upper step. Regarding the question of acceleration. Imagine you were strapped into a chair with the escalator stairs going beneath you. Imagine your only obligation were to let your feet keep up with the pace of the escalator stairs, while maintaining a force of however many lbs. you weigh. That's what I think it feels like when I'm trying to stay "stationary" on the escalator steps. I'm not going up, and there's no mgh. (In reality, I probably bounce up and down a little, and do maybe 30% the work of climbing a stationary stair.) When I go up fixed steps, the force in my legs is much more than the number of lbs. I weigh. It's the amount of lbs. I weigh plus the massxacceleration it takes to move me up to the next step at whatever rate I rise. But never mind my theory. I'd love to verify this by experiment. One way to do this would be to find a couple of small scales that we could strap to our feet and attach to some kind of data accumulator. Integrate the weight over time, and there you go: work! |
| Comment #2 from Phil (marsosudiro) 2009 Sep 27 - 11:07 pm : # |
| BTW: I really like your illustrations! |
| Comment #3 from Ken (realkato) 2009 Sep 28 - 8:25 am : # |
| I made that "center of mass not moving" argument initially as well, but again, you have to think acceleration, not motion. On an escalator, your center of mass may not be moving, but on a staircase, your center of mass is moving upward at a constant velocity. In both cases, a difference in forces (thrust versus gravity) is required to change that velocity; to maintain the velocity, you must provide upward continuous force equal to mg. The "strapped to the chair" argument is the same as the "handrail" argument. The only way that's equivalent to a staircase is if the staircase is equipped with a moving chair that you can ride upwards, moving your feet along with the steps. If there's a chair that's stationary, your butt creates the necessary force needed to keep yourself from decelerating back to -v without any effort, so that's kind of cheating. In fact, you could simply lift your feet completely off the escalator, and stay still with zero effort. I don't think you can argue that it takes zero effort to keep up with the down escalator if you were climbing it. |
| Comment #4 from Phil (marsosudiro) 2009 Sep 28 - 8:09 pm : # |
| OK, I'll say "center of mass not accelerating" :-) Also, I know that my chair analogy isn't very clear. It's not the same as the handrail equivalent because I asked the user to maintain force on the steps (via the feet) equal to the person's weight. The person would probably need a seatbelt to prevent lifting off the seat. My analogy wasn't about the person being supported, but rather to illustrate the idea of the center of mass not moving (or accelerating). But anyway -- here's another way of looking at how I see the moving escalator thing: imagine that you're standing on a fixed stairway, both feet on one step. Now take your right foot and touch the step below. Then pick it up and touch the step above. Then rest it again on the central step. Repeat with left foot. During the whole process, don't let your center of mass move up or down. This, I think, would duplicate the effort of doing the escalator walk. And it would be less than actually moving up the stairs. Hennyway -- I'd really like to see the experiment done! Also -- do you recall one of the early chapters from "Surely You're Joking, Mr. Feynman"? While a first year grad student in physics, he and some friends got into a discussion about a particular experiment whose outcome should be OBVIOUS. Problem was, it could be obvious in two opposite directions, depending on how you asked the question. So he did an experiment to find out. And refused to tell us (in the book) what happened. |
| Comment #5 from Tim Ross (Guest) 2009 Sep 28 - 8:46 pm : # |
| To me the answer seems obvious, but my argument is less.... mathamagical. I just figure that if you are moving, but not accelerating, then your body cannot feel the movement (see the elevator analogy). If your body cannot tell you are moving then any action you take in relation to objects traveling along with you must be no different then the same action if you and all objects were stationary. |
| Comment #6 from Ken (realkato) 2009 Sep 28 - 8:54 pm : # |
| Phil, my point about acceleration is that there is zero acceleration in either the case of the escalator or the stair, and the only way that can happen is if the person is applying a force equal to their weight in the upward direction. And I don't think the "touch the step below and touch the step above" is anything like walking up a down escalator. The laws of physics don't support your argument, I'm afraid. And keep in mind that I was firmly on your side until I did the math and convinced myself otherwise. I have thought about doing the experiment, but the force sensors and software needed to do it are a bit pricey. And there's also the problem of finding an escalator do this on, without being arrested by a mall cop. |
| Comment #7 from Phil (marsosudiro) 2009 Sep 29 - 12:24 am : # |
| You find the equipment, and I'll find the escalator :-) |
| Comment #8 from Phil (marsosudiro) 2009 Oct 2 - 4:21 pm : # |
| OK, so I just thought about it again. No math. But thinking about the powered climbing wall that used to be at my gym. Thinking about the mechanics of staying on the wall let me "feel" the math in a different way. And.. Now I agree with you. And I'd still like to do the experiment :-) |
| Comment #9 from Phil (marsosudiro) 2009 Oct 8 - 10:27 am : # |
| Related-ish: "Can you get more people to take the stairs by making it fun?" http://www.youtube.com/watch?v=2lXh2n0aPyw |
| Comment #10 from Ivan (Guest) 2009 Oct 29 - 2:30 am : # |
| Hello, it's curious thing, but recently I argued with my friends on the same thing. I think there will be difference. Namely, there will be the difference in that fact that in the case of escalator we apply force to move up only legs with every step, but not all the rest body. Just because of "flexible" construction of body we almost maintain position of the center of mass. Of course, to maintain our vertical velocity, there should be a vertical force equal to mg, as mentioned in the discussion, but doesn't it seems that in the case of stairs every step we lose accumalated power becase of gravity and should apply force mg + delta (if there will be no delta we will stop!) with the next step, while in the case of escalator only mg? So my point is that it seems to me that when we would try to make a step "up" on the escalator we would not experience the same exersize, like in the case of stairs, because we would rather compensate the job of escalator on moving only our legs down rather than the whole body, you will apply less force to you forward leg, just folow it down with escalator and do not have to apply additional energy to accelerate your body as whole against the gravity. And it's rather doubtfull that those additional energy will be used to accelerate escalator and in electrical load changes, because of its' colossal mass.. the same is when you ride a bike only very small part of engine power will rotate the Earth.. |
| Comment #11 from Ivan (Guest) 2009 Oct 29 - 3:23 am : # |
| Anyway, idea with the experiment sounds great.. |
| Comment #12 from Ken (realkato) 2009 Oct 29 - 9:12 am : # |
| In the model I presented, I assumed that you provide a constant force equal to mg. If your initial motion is upward and you are providing a constant upward force equal to mg, you don't "lose accumulated power"; your velocity only changes if the net force (your upward force minus the downward force of gravity) is non-zero. That's basic Newtonian physics; a body in motion tends to stay in motion. In your argument, on the stairs, you're assuming that you decelerate and re-accelerate with each step (which is a reasonable real-world model). That means that for a period of time (as you're landing), you apply force "mg - delta", and that for a period of time (as you're stepping), you apply force "mg + delta". And yes, if you don't apply force "mg + delta" to re-accelerate, you will stop. But with that model, on the escalator, it's precisely the same thing. You make the same bodily motions. If you don't apply force "mg + delta" to re-accelerate yourself with each step, then you will lose velocity relative to the escalator, and you will end up riding the escalator down. And yes, the amount of energy that you apply to an escalator is relatively small compared to the escalator's overall kinetic energy, but the amount of potential energy you gain by climbing stairs is also relatively small compared to that. I'm pretty sure I'm right on this. I'd be willing to try the experiment if I can drum up the equipment. But I'd also like to see a mathematical counter-argument, if someone can come up with one. |
| Comment #13 from Ken (realkato) 2009 Oct 29 - 9:25 am : # |
| I meant to post and diagram this in a followup article, but: as far as the energy you exert on the escalator, with each step, you're exerting force "mg / sqrt(2)", vectored diagonally downwards, on the escalator as it moves a diagonal distance "h * sqrt(2) / n", where h is the overall height of a flight of stairs, and n is the number of steps in that flight. In physics, the amount of energy you put into something is called work, and the formula is "w = Fd" (work equals force times distance). The mass of the escalator is irrelevant in this calculation. So with each step, the amount of work you put into the escalator is "(mg / sqrt(2)) * h * sqrt(2) / n", which reduces to "mg * h / n". Over n steps, the total amount of work you've done is "mg * h"... which is precisely the potential energy you'd gain if you climbed a flight of stairs. |
| Comment #14 from Ivan (Guest) 2009 Oct 30 - 2:43 am : # |
| Well, i think, I have one. Formally, as you mentioned, the work is w = Fd. First, let's calculate the work, that you is putting into the stairs while lifting your body up. You are applying the same force to it mg / sin(a) and moving the same distance with respect to stairs, byt my answer is: almost zero. If the staircase is massive and is hardly connected with ground we can do not take it consideration and all energy we apply is exerted to climb our body up. Why in the case of escalator it should be another value? What about accelerate-deaccelerate model, it seems to me, that in the case of escalator every step we have to accelerate only legs, but not the whole mass of out body. Other words only a part of our body is involved by escalator down, and of course we should compensate it, but it will be less than work if escalator would move us (as whole) to it's base and than we will climb up using stairs. While in the case of stairs we have to do it, otherwise we won't climb or lose balance. |
| Comment #15 from Ivan (Guest) 2009 Oct 30 - 3:02 am : # |
| About w = Fd, it's exactly that we want to know. But we should calculate it correctly. What I mean. Lets imagine an inertial frame of reference (IFR) linked with a man who climbs stairs up. Although d = 0 in this IFR, the work is not zero, right? That's because actually in this case d should be counted with respect to earth, it's invariantly and the balance of energy should be kept! So, if we do not input power into escalator and do not move up with respect to ground we will gain less efforts.. |
| Comment #16 from Ken (realkato) 2009 Oct 30 - 8:00 am : # |
| You do put power into the escalator. Imagine if the escalator were a non-motorized very-low-friction device. You'd find it awfully difficult to climb it, even if it were pretty massive, because with each step you'd accelerate the escalator belt in the other direction. The work that you do when you climb a flight of stairs is mgh (your force is vectored diagonally, so it's "mg * sin 45", or "mg / sqrt(2)" for a 45-degree angle, but the distance you travel is "h * sqrt(2)", so the angle component cancels out). That makes sense, because that's the potential energy you've gained, as well. And as I showed in Comment #13, the work that you put into an escalator over the same number of steps is also mgh. As far as inertial frames of reference: on an escalator, the frame of reference is the escalator itself. Go back to the "large room with a staircase" example in the original post. Another example to consider: imagine walking the wrong way on a horizontal conveyor belt for ten miles. You do zero work on your own body. Does that mean you've expended no energy? |
| Comment #17 from Ron (Guest) 2010 Feb 19 - 11:34 pm : # |
| I like Tim Ross comment #5 the best. It is simple and accurate. Here's another way of looking at it, with no assumptions about acceleration and velocity, nor how your feet are moving. Suppose the escalator is not moving, and you climb from the bottom to the top. It is just like climbing a flight of regular stairs and you have expended energy equal to mgh where m is your mass and h is the vertical height. Your body now contains that amount of additional potential energy, relative to where you started. Now you stop at the top and remain still, while someone turns on the escalator and it carries you all the way to the bottom, where you started. Your potential energy has now returned to what it was before you started climbing. But clearly that does not negate the work you did in climbing the stairs. I think everyone would agree the exercise was the same as if you had climbed a regular flight of stairs. So where did that potential energy in your body disappear to, when the escalator carried you back down? That energy went into the escalator equipment. For example, if you supposed that the escalator had some kind of braking mechanism to keep it from accelerating, that braking mechanism (which could be a friction brake) had to expend additional energy to prevent the escalator from accelerating as it carried you down, and that additional braking energy is equal to the potential energy your body gave up when you returned to the bottom. One way or another, the potential energy you created in climbing to the top was returned to the escalator mechanism, in this case in the form of extra heat dissipation in the friction brake. The same effect would occur if you climbed one stair, then the escalator moved down one stair, then you climbed another stair, and the escalator moved down another stair. If you extrapolate this series of steps into continuous motion of both you and the escalator, the effect is still the same except the up and down motions become very small and you remain in the same vertical position. This is the same reason why walking on an inclined treadmill feels just like walking uphill. I'm sure Einstein would have an elegant explanation in terms of inertial reference frames, etc. |
Comments are closed for this post.
